

The answer is basically "not a chance". No Earthbound telescope can see the flag on the Moon. Why not? For openers, the Earth's atmosphere is never steady enough to allow resolution below about one arc second for most locations. Beyond that, the telescope required to "see" the flag would need to be absolutely huge! Here is some basic analysis to show what would be needed:
Method 1 will use simple proportions to show what would be needed. The Moon's diameter is approximately 2160 miles. The Moon is nominally about 239,000 miles from Earth, and at this distance it subtends a diameter of about 30 arc minutes in the sky as seen from Earth. There are 60 arc seconds per arc minute, so the Moon is about 1800 arc seconds across. Let's figure out how many arc seconds represent one mile. The calculation is straightforward: if 1800 seconds = 2160 miles, then 1 mile = .83 arc seconds (basically just divide 1800 by 2160).
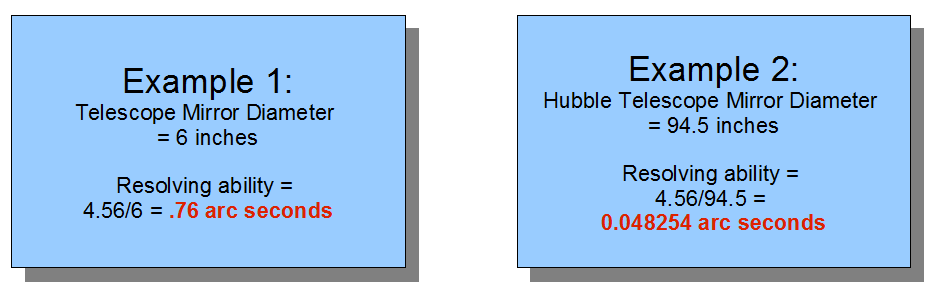
So, now we know that 1 mile is about .83 arc seconds. How big is the flag? I do not know for sure but let's assume it is 3 feet long on the long side. How many arc seconds is this? We know that 1 mile = .83 arc seconds; the flag is 3/5280 miles wide (or about 5.682e-4 miles). To find out the arc seconds, we simply multiply this value by .83 to get 4.716e-4 arc seconds. A long time ago someone named Dawes determined that the resolution of an optical telescope is basically 4.56 divided by the telescope's diameter (in inches). So, from that we can rearrange the equation to say that the diameter of the telescope needed (in inches) is 4.56 divided by the resolution required (arc seconds). Dividing 4.56 by4.716e-4 comes out to be 9669 inches. Converting this to feet yields about 805 FEET! And this would be the required telescope diameter to JUST BARELY see the flag at all! And, it would only be just visible as a small dot, it would not "look" like a flag at all.
Let's say we really want to see the flag and have it look like a flag. We'll have to make some assumptions again. Let's assume that the stripes on the flag are 1.5 inches wide and we want to just be able to see them. Using the same method as above we can come up with an answer. In this case we need to be able to see something that is 1.5/12/5280 miles wide, or 2.367e-5 miles. We multiply this by .83 to get the resolution (1.965e-5). Dividing 4.56 by this number yields 232065 inches, or about 19388 FEET! This value is also about 3.6 miles. Clearly it is not possible to build an optical telescope of this size. So, basically the Flag on the Moon remains "invisible" to us here on Earth.
Method 2 will use trigonometry to show the same basic result as above. If you do not have a background in basic trigonometry then this method may seem intimidating as we do show some basic math. As we previously mentioned, the Dawes
Limit for resolution of an optical telescope is as follows:

Below we examples of the formula for two different size telescopes:
In order to figure out what size scope we need to see the flag on the Moon we have to know how big the flag actually is. For purposes of this analysis we will assume that the flag is 3 feet wide. The diagram below shows some
information regarding the ratios of the dimensions of the American Flag:

We decided on using a flag width (dimension B in the diagram) of 3 feet (36 inches). Therefore A = 36/1.9 = 18.95 inches. Each stripe on the flag is 1/13th of A, so for our flag one stripe is 18.95/13 = 1.457 inches. we will round this up to 1.5 inches for purposes of our example.
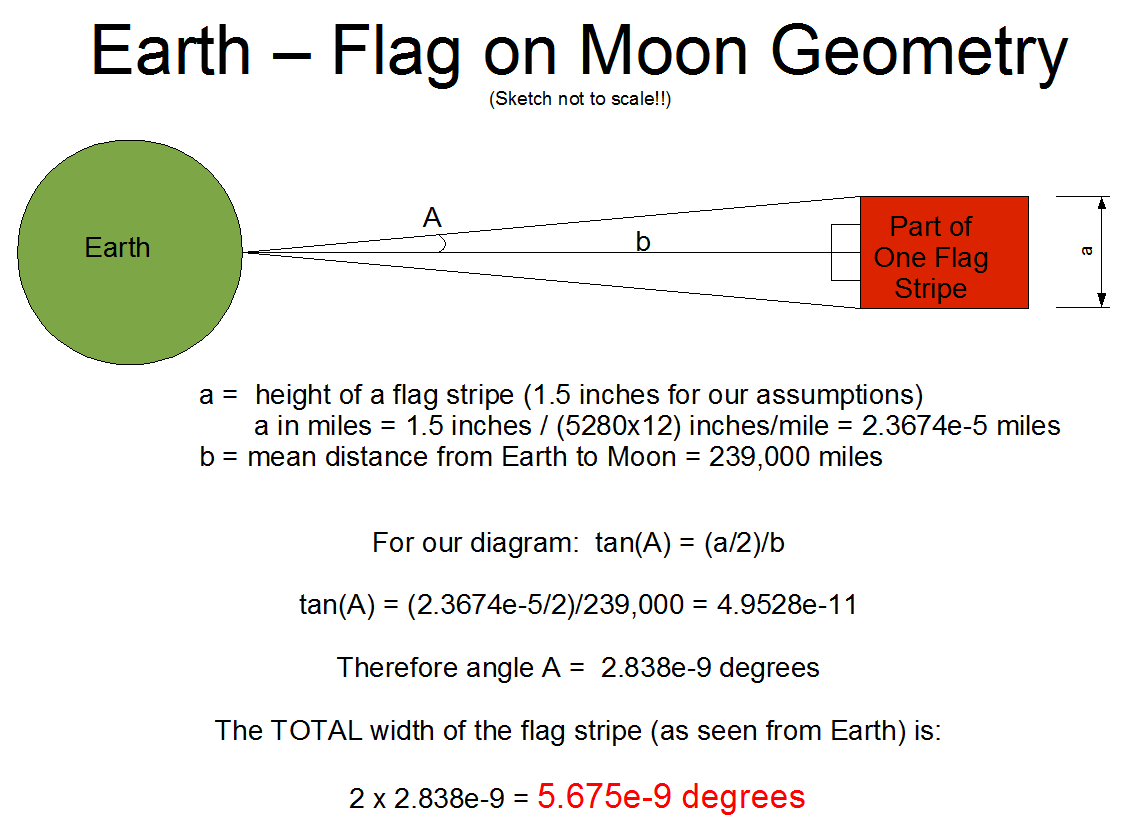
OK, now we have established that the flag stripe is 1.5 inches wide, so what size telescope do we need to see this? First we need figure out how many arc seconds the width of a flag stripe represents at the distance of the Moon.
Before we do that, let's take a look at the basics of the Earth-Moon geometry:
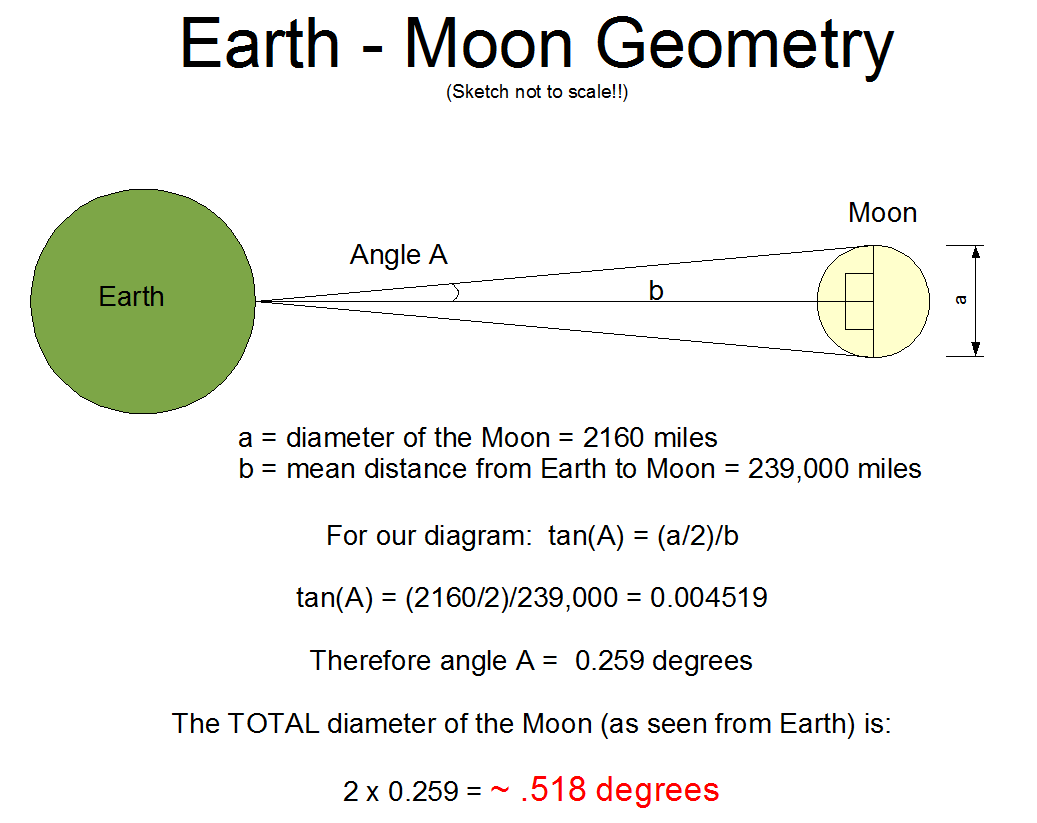
The above diagram shows that the Moon subtends an angle of a little more than half a degree. So how about the flag? Obviously it will subtend a much smaller angle. The following diagram shows the calculations for figuring
how many arc seconds one stripe of the American Flag subtends at the distance of the Moon:

As powerful as Hubble is (above the limits of the Earth's atmosphere), it has no chance of seeing the Flag on the Moon. What could it see? Well, Hubble has a mirror that is 94.5 inches in diameter. That gives it a resolution of 4.56/94.5 or about 0.0483 arc seconds. If one does the math, this translates to a resolution of about 295 feet at the distance of the Moon. So, Hubble could just detect an object that was 295 feet across on the Moon. To see any detail on an object, it would have to be somewhat larger. To put this in perspective, if a typical pro football stadium was located on the Moon Hubble could make out some basic details (the field could just barely be made out as a dot in the center of a very small oval).
Hubble is in orbit at a height of about 375 miles up. If we work the math, it can be shown that Hubble could just make out something that is 5.56 inches wide on Earth. Basically Hubble could just make out the size and shape of a car license plate (assuming it was laying flat on the ground). However, reading the numbers would be out of the question!
People who believe that the Moon landings were a hoax often raise the question "Why can't we see the flag on the Moon [from Earth] with our most powerful telescopes?". The analysis provided on this page shows that even Hubble not anywhere near powerful enough to see something the size of a flag (about 3 feet wide) when it is at the distance of the Moon. The laws of optics dictate that even Hubble's 94.5 inch mirror can never see such a small object at that distance. Even much larger Earth bound telescopes are far away from being capable of seeing the Flag! If you are someone who does believe that the Moon landings were staged, I most probably cannot convince you otherwise. Regardless of that, the analysis here clearly shows that seeing the flag on the Moon from Earth is not possible with any technology we have today.
Check out this story: LRO Sees Apollo Landing Sites. The reason this spacecract can see the landers is that it is MUCH closer to the Moon.
As of today, spotting the Flag on the Moon (from Earth using a telescope) remains impossible. The only method that could be used to (in theory) see something as small as the Flag on the Moon would be to use two optical telescopes set
(for example) 1000 miles apart. This would easily provide the required resolution, the huge problem however is combining the images from both telescopes in such a way to realize the resolution. As far as I know right now that
technology is not available. Even if the technology was available, the unsteadiness of the Earth's atmosphere would likely render the method useless.
Use your browser's "back" button, or use links below if you arrived here via some other path:
This page is part of the site Amateur Astronomer's Notebook.
E-mail to Joe
Roberts
Images, graphics and HTML text © Copyright 2007-2009 by Joe Roberts. Please request permission to use
photos for purposes other than "personal use".